
Kodlamalarda 19 sayısı dominant bir rol üstlenir. Ele alınan metnin bütününde ve doğal sırasında ortaya çıkan kodlamalarda öncelikle mod 19 = 0 denkliği aranır. Eğer bu denkliği sağlayan bir kodlama bulunursa, bu kodlamanın mesanisine, (Çiftine, Tersine, Tamamlayıcısına) bakılır ve mod 7 = 0 denkliğini sağlaması aranır. Mesanilerde mod 7 = 0 denkliğini sağlayan bir kodlama bulunursa, kriterler listesine eklenir.
Referans: 7-19 İKİZKOD kitabı / İMRAN AKDEMİR / www.ikizkod.com
15.Hicr Suresi’nin 87’nci ayeti Tekrarlanan İkilinin verildiğini ve verilen iki sayıdan birinin 7 olduğunu bildiren tek ayettir. Ayrıca bu ayet peygambere indirilen vahyin hem sayısal boyutunun hem de sözel boyutunun olduğunu beyan eder.
“Andolsun Biz sana Tekrarlanan İkili-den 7’yi ve Yüce Kur’ân’ı verdik.”
Bu ayette geçen “Yedi” kelimesi Kur’ân’daki diğer “Yedi” kelimelerinden farklı bir biçimde kullanılmıştır. Kur’ân’da onlarca defa yedi gök, yedi sümbül, yedi kişi veya yedi kapı gibi ifadelerde kullanılan “yedi” kelimesi “seb’a” (سبع), “seb’etu” (سبعة) gibi formlarla kullanılmışken Hicr Suresi’nin 87’nci ayetinde farklı ve özel olarak “seb’an” (سبعا) formuyla zikredilmiştir. Bu farklılığın nedeni ise “seb’an” formunda “Yedi” kelimesinin 19 sayısıyla direkt olarak sayısal bir bağ kurmasıdır. Yani “Seb’an” formunda yazıldığında “yedi” kelimesinin sayısal değeri 133 (7×19) olmaktadır.
133 sayısı 7 ve 19’un ilk ortak katıdır. Yani 133 sayısından önceki hiçbir doğal sayı hem 7’ye hem 19’a bölünmez. Referans ayette iki şeyin verildiğine değinmiştik. Birincisi tekrarlı-ikili sayısal bir sistem diğeri ise bu sayısal sistem ile kuşatılmış olan Büyük Kur’ân’dır. İşte ayette sayısal bir sistemin verildiğini bildiren cümledeki kelimelerin sayısal değerlerini incelediğimizde ayetin öne sürdüğü 7 sayısıyla tam bir uyum içinde olduklarını görürüz. Referans ayette sayısal sistemin verildiğini bildiren cümlenin sayısal değeri 1477’dir. (7×211)
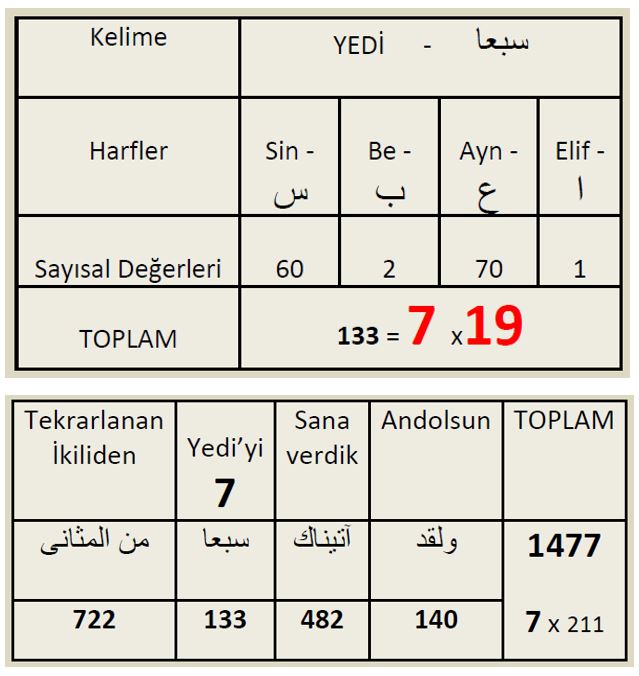
1477 sayısının rakamları toplamı ise 19’dur.(1+4+7+7= 19)
Ayrıca bu kelimelerin sayısal değerlerinde öyle bir ahenk bulunmaktadır ki kelimelerin sayısal değerlerinin iki yönlü ardışık dizilimleri 7’nin tam katını vermektedir.
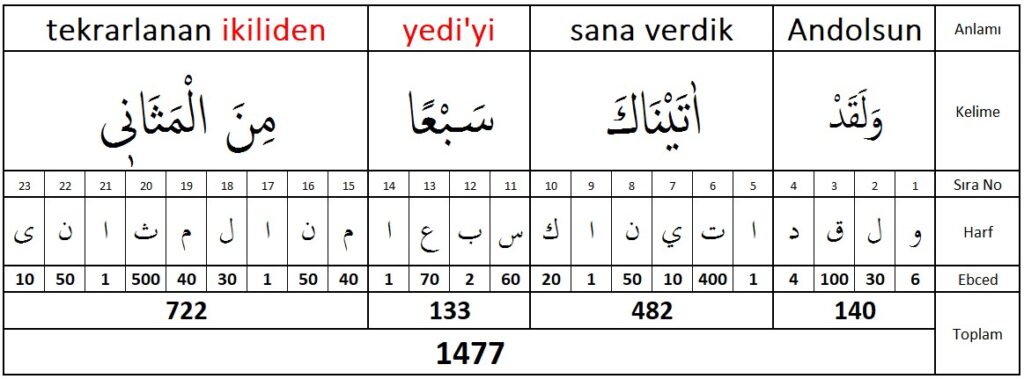
Kelimelerin sayısal değerlerinin soldan sağa doğru ardışık dizilimleri:
722 133 482 140 = 7 x …
Kelimelerin sayısal değerlerinin sağdan sola doğru ardışık dizilimleri:
140 482 133 722 = 7 x …
Cümledeki harflerin toplamının da 7’nin katı olması ve bu toplamın rakam değerlerinin 1+4+7+7=19’u vermesi işi biraz daha zorlaştırmaktadır. Bir insanın yukarıdaki oluşumun bir benzerini gerçekleştirmek için ne kadar uğraşabilir ki? Sayısal olarak başarsa bile oluşturacağı kelimeler anlamca uyuşmayacak ve çıkmaza girecektir; sayıları denkleştireyim derken kelimelerin anlamı bozulacak, kelimeleri uyarlayayım derken kelimeleri oluşturan harflerin sayısal değerlerinde bozulmalar olacaktır.
Referans sonu: 7-19 İKİZKOD kitabı / İMRAN AKDEMİR / www.ikizkod.com
—– 15 – Hicr Suresi – Ayet 87: —–
وَلَقَدْ آتَيْنَاكَ سَبْعًا مِّنَ الْمَثَانِي وَالْقُرْآنَ الْعَظِيمَ
https://quran.com/15/87 15:87- Andolsun ki, biz sana tekrarlanan yedi âyeti (Fatiha’yı) ve yüce Kur’ân’ı verdik.
15.Hicr Suresi 87. Ayet’in 7 kodlama sayısını tanımlayan kelimelerinin sayısal analizi
Ayetin ilgili kelimelerinin sayısal değerlerinde ortaya çıkan 7 kodlamaları son derece dikkate değerdir.
İmran Akdemir tarafından ortaya koyulan diğer kodlamalar:
Ayet harflerinin ebced değerlerinin ardışık sıralaması
6 30 100 4 1 400 10 50 1 20 60 2 70 1 40 50 1 30 40 500 1 50 10 ≡ 0 (mod 7)
Bu sayının, basamaklarındaki sayıların ters dizilimi de 7 kodlamasını doğrular
01 05 1 005 04 03 1 05 04 1 07 2 06 02 1 05 01 004 1 4 001 03 6 ≡ 0 (mod 7)
Ek olarak bizim vurgulamak istediğimiz bir diğer kodlama 2 kalanı vererek önem kazanıyor.
Ayet harflerinin ebced değerlerinin ardışık ters sıralaması
10 50 1 500 40 30 1 50 40 1 70 2 60 20 1 50 10 400 1 4 100 30 6 ≡ 2 (mod 7)
Kelimelerin ebced değerlerinin iki yönlü ardışık dizilimlerinin de 7 kodlamasını doğrulaması matematiksel bir özellik olmakla beraber, incelediğiniz zaman fark edebileceğiniz gibi, çok özel ve sadece 7 vurgusu yapan bir matematiksel özellik olduğunu görebilirsiniz. Bu matematiksel özelliğin tam da bu noktada ortaya çıkması, bence tesadüf olarak nitelendirilemeyecek bir durumdur.
140 482 133 722 = 7 x … 722 133 482 140 = 7 x …
Dört grup halinde ortaya çıkan, üç basamaklı sayılar. İlk görünüşte basit gibi gelebilir, fakat bu matematiksel özellik veya zorunluluk, 7 vurgusu için mükemmel uyumludur. Hatta özellikle yedi vurgusu için seçilmiştir dersek abartmış olmayız.
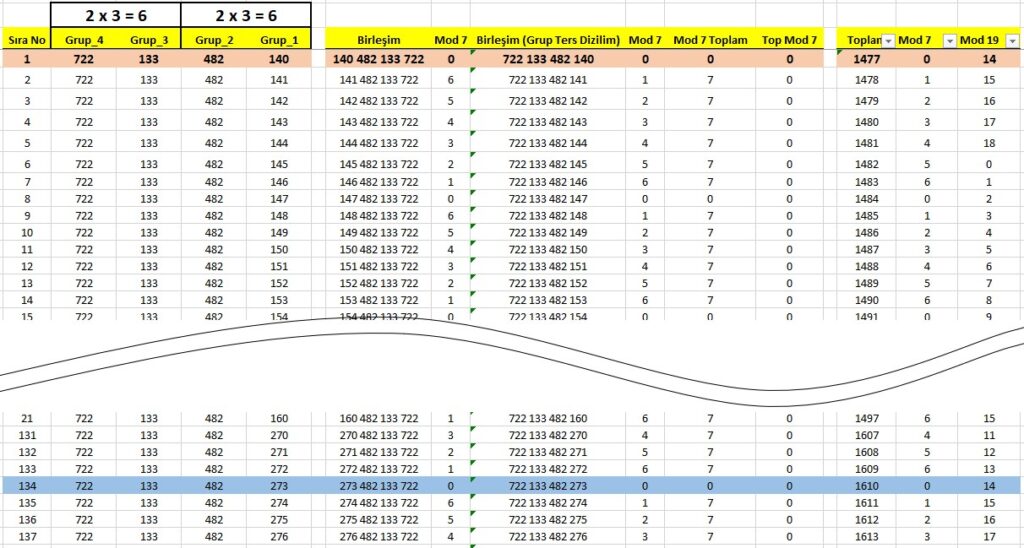
İlgili tabloları aşağıda veriyorum. Beraber inceleyelim.
Bu tabloda sayı yapısını incelemek için, öncelikle sayıyı bir dizi halinde ele aldık. Sayıyı bir arttırarak sayının yapısının nasıl değiştiğini, nasıl bir çevrime sahip olduğunu anlamaya çalıştık. Sayısal sistemleri inceleyen diğer görüşler, kodlama sayılarının bölümü sonucunda sıfır kalanına { ≡ 0 (mod 7) ve ≡ 0 (mod 19) } konsantre oldukları için bu ayrıntıları maalesef kaçırıyorlar. Sayı yapısındaki 7 vurgusu, kalan değerlerinin toplanmasıyla ortaya çıkıyor. 7 vurgusunu “Mod 7 Toplam” kolonunda çok açık bir şekilde görmekteyiz. 7 vurgusunun çıkması için sayı yapısının mutlaka 3 basamaklı sayılardan oluşan grupların, ikili olarak bir araya gelmesi gerekmektedir. Diğer tabloları incelemeniz için aşağıda verdim.
Ek olarak; Ayet kelimelerinin ebced değerlerinin oluşturduğu sayı örneği, yukarıda verdiğim tablonun çok kritik bir yerinde yer aldığını göstermek isterim. Bu noktada sayıların toplamı 1477’dir. Kodlama detaylarını görebilirsiniz.
1 + 4 + 7 + 7 = 19 ve 1477 ≡ 0 (mod 7) ve 1477 ≡ 2 x 7 (mod 19)
3 basamaklı sayılardan oluşan 2 grup, sayı yapısının 7 vurgusunu takip edebilirsiniz.
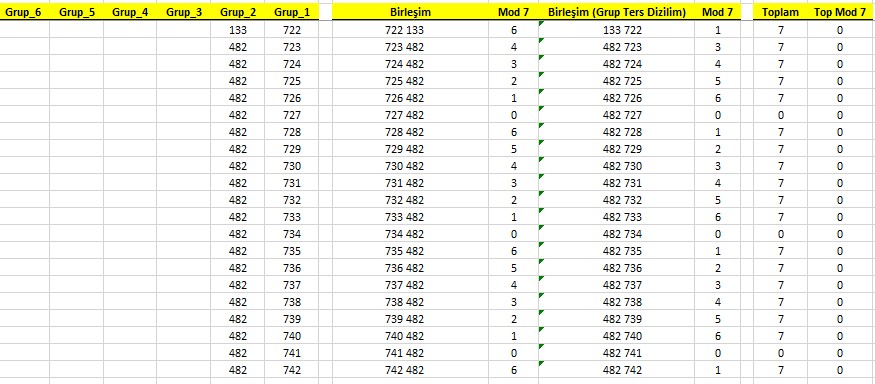
3 basamaklı sayılardan oluşan 6 grup,(2×3); sayının yapısındaki 7 vurgusu devam ediyor.
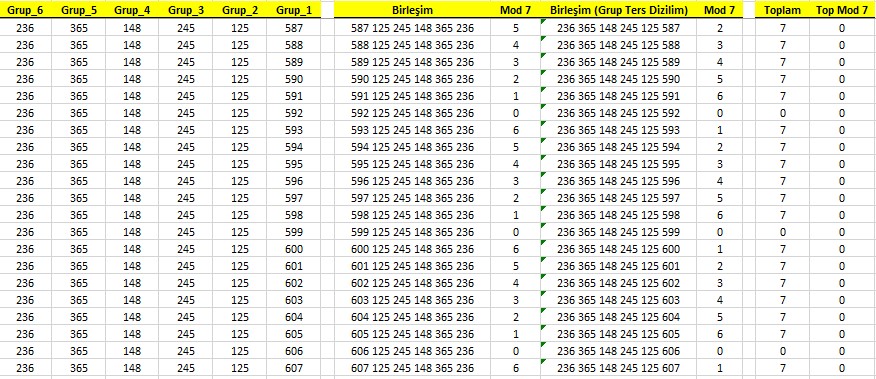
Yukarıda sözünü ettiğimiz 7 vurgulamasının 2, 4, 5 ve 6 basamaklı sayılardan oluşan grupların bir araya gelerek oluşturdukları sayı yapılarında olmadığını aşağıdaki tablolardan çok net bir şekilde görebilirsiniz.
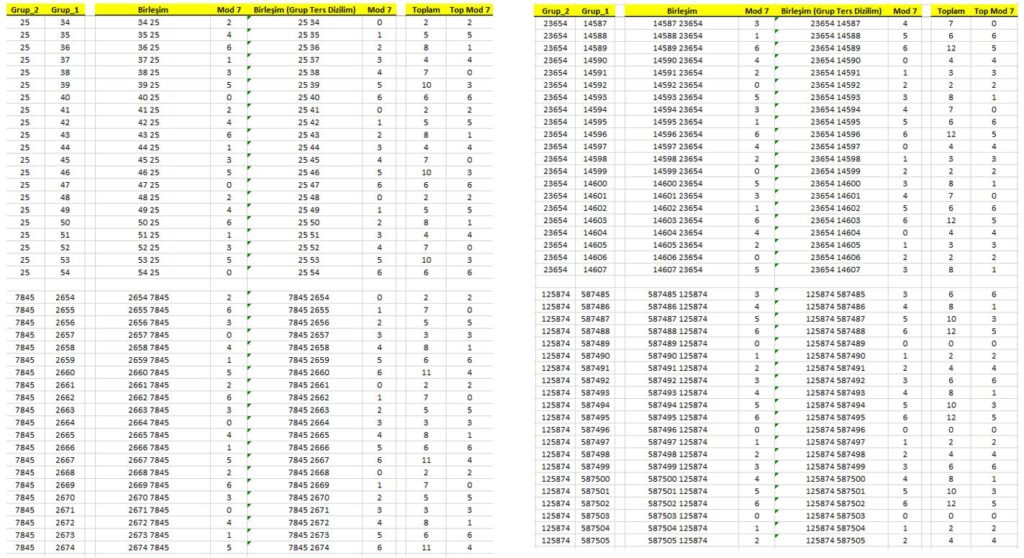
Sonuç olarak; 15:87 ayetindeki ilgili kelimelerin ebced değerlerinin oluşturduğu, 3 basamaklı dört gruptan oluşan bu sayı yapısı, 7 vurgusunu yapan çok özel bir matematiksel yapıya sahiptir.
140 482 133 722 ≡ 0 (mod 7) 722 133 482 140 ≡ 0 (mod 7)
Ayrıca; sayıların toplamı olan (140 + 482 + 133 + 722) 1477 sayısındaki kodlamalar da dikkate değerdir.
1 + 4 + 7 + 7 = 19 ve 1477 ≡ 0 (mod 7) ve 1477 ≡ 2 x 7 (mod 19)

Merhaba yaptiginiz calisma icin basta size cok tesekerur ederim .
fakat 2×3 yazili olan bolumu pek cozemedim acikliyabilirmisiniz tesekurler
Yazılan her hangi bir tamsayı 7 ye tam olarak bölündüğü de, tersinin de 7’e tam olarak bölünmesi için, 3 basamaklı sayılardan 2’li gruplar olması gerekiyor,
(2×3) 3 basamaklı 2 grup anlamına geliyor.
3 basamaklı sayılar bu şekilde 2’li gruplar halinde yazıldığında ve 7’ye tam olarak bölündüğünde, sayı tersten yazıldığında oluşan yeni sayı da yine 7’ye tam olarak bölünüyor.
Bu şekilde oluşan sayılar, düz olarak ve ters olarak yazıldığında, 7’ye bölümleri tam değilse, kalanlarının toplamının 7 olduğunu görebilirsiniz.
Bu bir matematiksel özellik olarak karşımıza çıkıyor.
3 basamaklı 2’li gruplar olmaz ise böyle bir özellik görünmüyor.
Hocam, yazdıklarınıza ek olarak, ayrıca سَبْعًا مِنَ الْمَثَانٖى ifadesinin kendisi de hem 7’ye hem 19’a hem de 2’ye işaret ediyor. Şöyle ki:
Bu ifadenin anlamı “2’liden 7’yi” demek. Bu yönüyle 2 ve 7 vurgusu zaten anlamsal olarak karşımıza çıkar. Yanı sıra bu ifadenin ebced değeri olan 855 de 19’a kalansız bölünüyor, buradan hareketle 19’a da bir işaret olduğu rahatlıkla söylenebilir.
Değerli tespitleriniz için teşekkür ederim. Allah razı olsun.