
Metin benzerliğinin ölçülmesi için, Kodlamaların oluşturulmasındaki kurallar:
1- Bütünsellik: Kodlamalardaki sayılar benzerlik ölçümü yapılan metnin tamamını kapsamalıdır. Örüntü göstererek bütünsellik ihlal edilebilir.
2- Dizilim: Kodlamalardaki sayılar benzerlik ölçümü yapılan metnin verdiği sırada olmalıdır. (Düz dizilimde kodlama varsa Ters dizilim kullanılabilir.)
3- Ölçüt: Kodlamalar mod 19 = 0 denklik kümesinde olmalıdır. ( Mesani olarak mod 7 = 0 varsa alınır. )
Çift ve Tek simetri kodlamalarının oluşturduğu denklik veya eşitlikler benzerlik ölçütü olarak alınır.
Ölçüt genel olarak tanımlanmıştır. Ölçütteki 19 ve 7 asal sayıları ve 0 denklik kümesi zorunlu değildir, istenirse başka bir asal ve mesanisi olan yine başka bir asal sayı ve başka bir denklik kümesi seçilebilir.
Mesani: İkililer, Çiftler, Sarmal. (Çifti, Eşi, Tersi, Tamamlayanı, Diğer parçası)
Yukarıda verdiğim kurallar çerçevesinde oluşan, metnin bütününü kapsayan ve metnin verdiği sıralamayı ihlal etmeyen düz diziliminde kodlama olan sayı dizileri ve bu sayı dizilerinden türemiş diğer sayı dizileri ve metnin ortaya koyduğu sayılar kullanılarak yapılan aritmetiksel işlemler ile türetilen sayı dizilerinin oluşturduğu kodlamalar kullanılabilir. Aritmetiksel işlemlerin sadece toplama işlemi olabileceğini burada belirtmek isterim, çünkü diğer aritmetiksel işlemler metinde olmayan sayıları bir veri yani, kodlama elementi olarak kullanmak anlamına gelir. Örnek vermek gerekirse, 4. kelimenin 6 harfi olduğunu düşünelim bu iki sayıyı metin bize verir. Bu sayıları toplayarak yeni bir sayıya ulaşabiliriz 4 + 6 = 10 ve bu sayıyı/kodu kullanabiliriz. Fakat bu iki sayıyı mesela çarptığımızı düşünelim 4 x 6 = 24 sayısına ulaşırız. 24 sayısı metnin karakteristiğini yansıtan bir kod değildir, çünkü metinde olmayan sayılar ile üretilmiştir.
4 x 6 => 4 + 4 + 4 + 4 + 4 + 4 veya 6 + 6 + 6 + 6 gibi açılımını yaptığımızda 6 tane 4’ün veya 4 tane 6’nın karşımıza çıktığını ve bu sayıların metin tarafından bize verilmediğini fark ederiz. Dolayısıyla, çarpma aritmetiksel işlemi vb. metinde olmayan sayıları kullanan aritmetiksel işlemler manipülatif bir kodlamaya bizi götürür, metnin karakteristiğini yansıtmaz. Sadece kodlama yapmak için keyfi yapılmış bir işlem olur.
Metnin barındırdığı sayısal değerler ile yukarıda verdiğim kurallar çerçevesinde yapılan kodlamalar metnin matematiksel karakteristiğini barındırdığı için metnin benzerlik ölçümünde nesnel, objektif bir kriter olarak kullanılabilir. Düz diziliminde kodlama bulunmayan metinler üzerinde Ters dizilim ve aritmetiksel işlemler ile türemiş kodlamalar metnin öz karakteristiğini (kelime ve cümle yapısının matematiksel karakteristiğini) yansıtmadığı için kullanılamazlar. Metnin matematiksel özellikleri arasından yukarıdaki ölçütü sağlayan kodlamalar seçilerek benzerlik ölçümü için kriptografik yapı oluşturulur. İki metnin benzerliğini ölçmek için oluşturulan kodlamalar arasında bir örüntü (matematiksel desen) bulunması gerekli değildir.
Yapılan iş: Bir yazının Kriptolojik olarak taklit edilebilirlik olasılık değerini ortaya koymaktır. Bu yöntem aynı zamanda, yazının kriptolojik karakteristiğinin de benzerliğinin ölçülebilmesini sağlamaktadır.
Bu nasıl yapılır? Bunun yöntemi nedir?
İlk olarak yazının belirteçlerinin sayısallaştırılması ile matematiksel karakteristiği ortaya çıkarılıyor;
Örnek bir kriter grubunun oluşturulma aşamalarını aşağıdaki gibi sıralayabiliriz:
1- Frekansı en yüksek veya yazının öne çıkardığı iki sessiz harfin yazının bölümlerindeki frekansları tablo halinde çıkarılıyor,
2- Yazının bütünselliği ve doğal dizilimi ihlal edilmeden, kodlamalar elde ediliyor,
3- Bütünselliği ve Doğal dizilimi ihlal eden fakat varsa, örüntü barındıran kodlamalar elde ediliyor,
4- Varsa, İkincil (mesani) kodlamalar elde ediliyor, (Düzü varsa, Tersine de bakılır. Mesani)
5- Yine varsa aritmetiksel işlemler kullanılarak türemiş kodlamalar elde ediliyor,
6- Biri dominant, diğeri ikincil (mesani) olarak, olasılık yoğunluğu bölgesini oluşturan 7 ile 29 asalı arasındaki asal sayılar kullanılarak, kodlamaların bütün denklikleri oluşturuluyor; (2, 3 ve 5 asalları seçici özelliğe sahip olmadığı için kullanılmazlar.)
7- Bütün oluşturulan denklikler içinden aynı denklik kümelerine giren dominant kodlamalar, ikincil (Mesani) denklikleriyle beraber Yazının Kriptolojik olarak taklit edilebilme olasılık hesabının oluşturuyor.
19 ve 7 sayıları, en düşük olasılık değerine sahip olduğu için Kur’an kodlamalarında ön plana çıkıyorlar.
Bu sayıların Kur’an ayetlerinde referans olarak verilmesi olayın fark edilmesini sağlamıştır.
Deneyerek kendi gözlerinizle görünüz. SONRA LÜTFEN DÜŞÜNÜNÜZ,
1400 sene önce, yokluğun, savaş ve ölümün kol gezdiği, ahlaksızlığın diz boyu olduğu bir ortamda, insanın tuttuğu kalem ile yazılmış ve çöl kumları içinden ortaya çıkmış bu kitapta böyle bir şey nasıl olabilir?
Bu olayı dünyadaki bütün insanların bilmeye hakkı vardır, Lütfen insanları bilgilendiriniz.
Kodlamaları anlamanın en iyi yolu, denemeler yaparak, mikro düzeyde benzer kodlamaları oluşturmaktır. Bu şekilde matematiksel zorluğu, olayların detayını çok kolay anlayabileceksiniz. 1. grup kodlamaları gözlemleyiniz sonra, 2. grup kodlamalar bölümündeki mikro kodlama denemelerini yapmanızı ısrarla tavsiye ediyorum.
1. Grup Kodlamalar:
11. kritere kadar olan birinci grup kodlamalar Ha ve Mim surelerindeki kodlama harf sayılarının toplamları üzerinde oluşan kodlamalardır.
Bu kodlamaların doğal iterasyona göre
(sayıların birer birer arttırılması vasıtasıyla, anlayanlar için i++; olarak )
hesaplanan Toplam Varyasyon sayısı 843 Kentilyondur.
Bugün kullandığımız bilgisayarlar ile yaklaşık olarak 535 milyon yılda taranabilir.
Sofistike algoritmalar kullanılırsa daha kısa sürelerde istenilen kodlamanın benzeri (misli – dengi – katları) bulunabilecektir. Olayın zorluğunu anlayabilmeniz için denemeler yaparak, kendiniz görmeniz gereklidir. Birinci grup kodlamalarda 1. kriterden başlayarak ve üzerinde düşünerek kriterleri sağlayan kendi sayılarınızı bulmaya çalışın. Olayı hemen anlayacaksınız. Zorluğu hemen göreceksiniz.
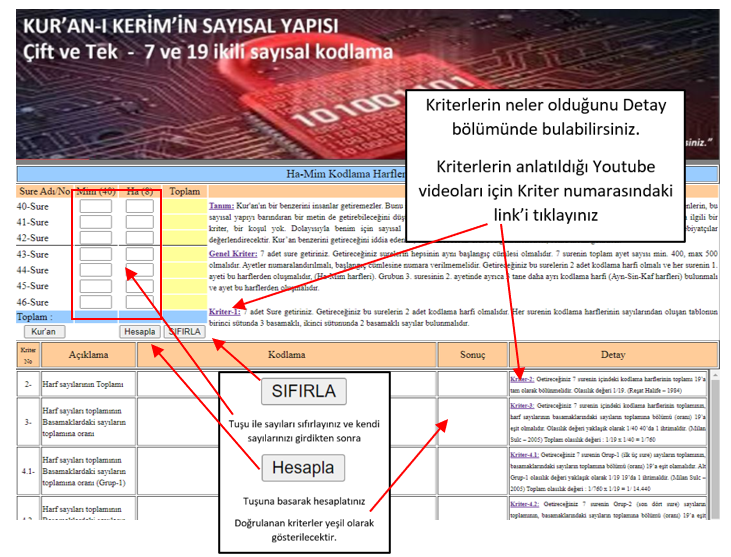
1. kriter tabloya 3 basamaklı ve 2 basamaklı sayıların girilmesidir ve basit olarak yapılır. 2. Kriter de çok basittir. Sadece sayıların toplamını 19’un katı yapmanız yeterli olacaktır. 3. kriter sizi zorlamaya başlayacaktır. Olayın gerçekten zorlaştığını ve nasıl yapacağınızı bilemediğinizi, daha derin düşünmeniz gerektiğini iyice görmüş olacaksınız. Kendinize bu fırsatı verin. Biraz bu noktada zaman harcayın. Harcadığınız zamana üzülmeyeceksiniz. Sizi temin ederim.
4.1, 4.2, 4.3, 4.4 kriterlerini ve diğerlerini bilgisayar programı kullanmadan bence yapma imkanınız yoktur. Bilginiz olsun.
“Tesadüf” tuşunu kullanarak sayıları bilgisayarın rastgele üretmesini sağlayabilirsiniz. Bu şekilde denemeler yaptığınızda, olayın tesadüfen tutturulamayacağını, bu sayısal yapının bir tesadüf eseri olamayacağını hemen anlayabilirsiniz. Sayılar üzerinde deneme yanılma yaparak diğer kriterlerden bazılarını tutturmanız, sizin de kabul edeceğiniz gibi, bir anlam ifade etmemektedir. Burada önemli olan kriterleri sırasına göre hepsini tutturmaktır. Ve olayı bilinçli olarak yapmaktır.
Çözümü olan ve içinde düzen barındıran
bir karmaşıklığı
varyasyonlarını taramadan
insan ortaya koyabilir mi?
İşte soru budur.
Karmaşıklık, karmaşa veya kompleksite: İlişkilerinin anlaşılması ve tanımlanması güç parçalardan oluşan bir sistemi tanımlama yöntemine verilen addır.
Karmaşıklık genellikle ‘sistem‘ kavramı temel alınarak tanımlanmaktadır. Bu kavramların büyük bir bölümü karmaşıklığın, bir sistem içinde yer alan öğelerin durumu ve bu öğeler arasındaki ilişki biçimlerini ortaya koyduğunu kabul etmektedir.
Karmaşıklığı oluşturma ve arttırma gücü, kavramsal olarak koleksiyonlararası ilişkilerdeki çok sayıda varyanslara bağlıdır. Bazen de bu ilişki dışında bağımsız olan elemanlararası koşulların, eleman bağımsızlığından kaynaklanan ilişkileri varyansları azaltır. Böylece ayırt edilir, monoton veya ilintili ilişkiler veya etkileşimler oluşur. Warren Weaver’in görüşüne göre karmaşıklık iki şekilde ortaya çıkar: düzenli ve düzensiz karmaşa.
Kaos Teorisi veya Kaos kuramı veya Kargaşa kuramı; yapısal olarak bir fizik teorisi ya da matematiksel bir tümevarım değil, fiziksel gerçeklik parçalarının bir bütün olarak eğilimini açıklamaya yarayan bir yöntemdir.
Birçok farklı girdinin sürekli değişerek fiziksel değişimler ve farklı düzenler yaratması ve bu düzenlerin yine kendisini etkilemesi insan zekasının ve günümüzdeki gözlem ve bilimsel tahmin yeteneklerinin çok çok üstünde olmasından dolayı kaos olarak nitelendirilir. Oysa tüm bu değişimlere neden olan fiziksel yasalara ve matematiksel açıklamalara hakimiz. İşte bu noktada karşımıza düzen ve kaosun aslında birbirine ne kadar sıkı sıkıya sarılmış olduğu ortaya çıkar. Fiziksel yasalar ne kadar basit olursa olsun sonuç o kadar rastlantısal ve karmaşa doludur.
Kendi anlayışıma göre “Karmaşıklık” tanımını vermeye çalıştım. Yukarıdaki sorunun pratik olarak yaptığım çalışmalarda mümkün olmadığını görüyorum.
DÜZENSİZ KARMAŞAYA şöyle bir örnek verebilirim: Elimizde tuttuğumuz bir cam bardağı, hızla beton bir zemine fırlattığımızı düşünelim. Cam bardak, zemine çarptığında kırılarak çok küçük diyebileceğimiz parçalara ayrılır. Bu olay bütün detaylarıyla incelenirse, taklit edilemez niteliktedir. Ben veya siz veya hiç kimse bu olayı tam olarak taklit edemez, benzerini yapamaz. Bu kırılmanın, parçalara ayrılmanın bütün detaylarını nesnel olarak ortaya koyabiliriz, gözlemler, ölçümler yapabiliriz. Taklit edilemezliğini, benzerinin yapılamayacağını olasılıksal olarak ortaya koyabilir, hesaplayabiliriz. Farkında mısınız, biz benzeri insanlar tarafından yapılamayacak bir şey yaptık. Biz insanız ve insanlar tarafından benzeri yapılamayacak bir şey yaptık. Çelişkili gibi gözüküyor değil mi? Fakat hiç de çelişkili değil, açıklayabilirim.
Olayın taklit edilemezliği bizden, yani insandan kaynaklanmıyor, aslında olayı biz yapmıyoruz. Cam bardak bizim elimizden çıktığı anda olayın kontrolü bizim bilincimiz dışına çıkıyor ve olay doğal kuvvetler tarafından bizim bilincimiz dışında gerçekleşiyor. Bundan dolayı taklit edilemez nitelikte. Eğer insan bilinci kırılma eyleminin her detayını tek tek yönetebilseydi, müdahale edebilseydi, işte o zaman biz yapıyoruz, insan yapıyor diyebilecektik. Fakat bu durumda yöntem ve bütün müdahale ayrıntısıyla belli olduğu için taklit edilemezlik ortadan kalkacaktı. Dikkatinizi çekerim, olay veya konu kendini göstermeye başlıyor. İnsan müdahalesi ve taklit edilemezlik bir arada bulunamıyor ?!!
DÜZENLİ KARMAŞA, aynı örnek üzerinden açıklandığında, bence bütün konu açığa çıkmış oluyor. Bakın şöyle bir akıl deneyi yaparak olayı anlatmaya çalışayım: Yine bir cam bardak var, hızla beton bir zemine fırlatıldığını biliyoruz ve cam bardağın, zemine çarptığında kırılarak yine çok küçük diyebileceğimiz parçalara ayrıldığını biliyoruz. Bu cam parçalarını çok yakından inceliyoruz. Üzerlerinde ölçümler yapıyoruz. Yaptığımız gözlem ve ölçümler sonucunda kırılan cam parçalarının içinden bazılarının çok belirgin bir şekilde altıgen, kare, dikdörtgen, eşkenar üçgen, daire gibi çok belirgin, çeşitli düzgün geometrik şekillerde olduğunu fark ediyoruz. Ölçümlerimizi arttırıyoruz ve bulduğumuz düzgün geometrik şekildeki parçaların gruplar halinde bazı bölgelerde yer aldığını hayretle gözlemliyoruz. Bu geometrik parçaların gruplar içindeki sayılarını bir tablo halinde listeliyoruz, dizilimlerini inceliyoruz, ortama dağılımlarını inceliyoruz ve ortaya çıkan sayısal değerler üzerinde ilginç matematiksel özelliklerin olduğunu fark ediyoruz. Olaya uzaktan baktığımızda, bir cam bardağın beton zemine çarparak kırılmasından ibaret olarak görüyoruz, fakat yakınlaştığımızda olayın içinde anlam vermekte zorluk çektiğimiz fakat kabul etmek zorunda kaldığımız bir düzenliliğin olduğunu gözlemliyoruz. Cam bardağın beton zemine çarptığı anda, kırılmasıyla ilgili insan müdahalesi veya bilinçli bir müdahaleyi göremediğimiz, tespit edemediğimiz bir durumda böyle bir karmaşıklığın içindeki bu düzene mucize diyoruz çünkü bunu bir insan yapamaz. Gerçek olmayan bu akıl deneyini bir metafor olarak görünüz, işte bu metaforda olduğu gibi benim Kur’an metni içinde gördüğüm ve ortaya çıkardığım sayısal yapı, insan kapasitesini aşan bir düzenin olasılıksal ifadesidir.
Çalışmalarım sonucunda Kur’an’da olan insanların yapamayacağı şeyi göstermiş bulunuyorum. 1400 yıldır Müslümanların yapamadıkları bir olaydır bu. Fakat henüz farkında değiller. Üniversiteler farkında değil, basın – medya farkında değil, hiç birisi farkında değil. Tanıtmaya çalışıyorum.
Aşağıda verdiğim linkte bulunan WEB sayfamdaki Düzen Barındıran Karmaşıklığı insanlar varyasyonlarını taramadan, bence ortaya koyamazlar. Neden? Çünkü, karmaşıklığı oluşturan her parça diğeri ile bir düzen dahilinde ilişkilidir. Parçaların düzen dahilinde bu ilişkilerini kurmak, varyasyonları tarayarak, uygun varyasyonu bulmakla mümkündür. Bu ilişkilerin varyasyonlarını doğal iterasyonla taramak 535 milyon yıl alıyor, yani ben bu durumu ortaya koyarken varyasyonları taramadım. Düzeni ve Parçaları Kur’an’dan hazır aldım, birleştirdim ve bu Düzenli Karmaşıklık ortaya çıktı. Sonra ciddi mesai harcamama rağmen birinci grup kodlamalar olan bu kısmın bile henüz bir benzerini getirebilmiş değilim.
Denemeler sonucunda kriterleri sağlayan sayıları bulan olursa aşağıya yorum olarak yazsın lütfen, herkes görsün. Ben kendi çalışmalarım sonucunda bilgisayarın doğal iterasyon olarak varyasyon tarama hızı olan saniye de 50 bin varyasyon tarama hızını bir algoritma geliştirerek yaklaşık 3.200 kat arttırdım ve çeşitli kısıtlamalar ve kabuller ile hareket ederek ilk 10 kriterin benzerini buldum, aşağıya yorum olarak yazıyorum, dileyenler kontrol edebilirler. Yaptığım algoritmayla saniyede 160 milyon varyasyon geçilmiş oluyor. Bu durumda bile, ne kadar kısıtlamalar ve kabuller yapsanız fayda etmiyor, 11 kriteri de sağlayan sayı dizisini bulmam için 36 yıl gerekli oluyor, dolayısıyla, şimdilik bulamadık. Belki ileride daha değişik bir algoritmayla çözümü sağlayabilirim. Fakat kriterler devam ediyor, dolayısıyla bütün sayısal yapının benzerini üretmek, bence insanlığın kapasitesini fazlasıyla aşmaktadır.
Buradaki matematiksel zorluğu görmeniz, fark etmeniz yeterli olacaktır. 2. grup kodlamaları da bu şekilde görüp denemeniz sizin için çok önemlidir, olaya bakışınızı büyük oranda değiştirecektir. Denemeler yapmanızı Israrla tavsiye ediyorum.
Denemelerinizi buradan yapabilirsiniz.
KUR’AN ORİJİNAL KODLAMALARI
Giriş Seviyesi – 1
Giriş Seviyesi – 2
Giriş Seviyesi – 3
Giriş Seviyesi – 4
Uzman Seviye – 1
Uzman Seviye – 2
Uzman Seviye – 3
Uzman Seviye – 4.1
Uzman Seviye – 4.2
Uzman Seviye – 5 *** Yazı Girişi ***
Yeni bir metin girerek Kodlamanın başka yazılarda olup olamayacağını
deneyerek, kendi gözlerinizle görebilirsiniz ….
Bu kodlamalar Kur’an orijinal kodlamalarıdır. Çok ciddi matematiksel zorluklar barındırırlar. Olayı anlayabilmeniz için aşağıda, denemeler yapabileceğiniz mikro örnekler hazırladım.
2. Grup Kodlamalar:
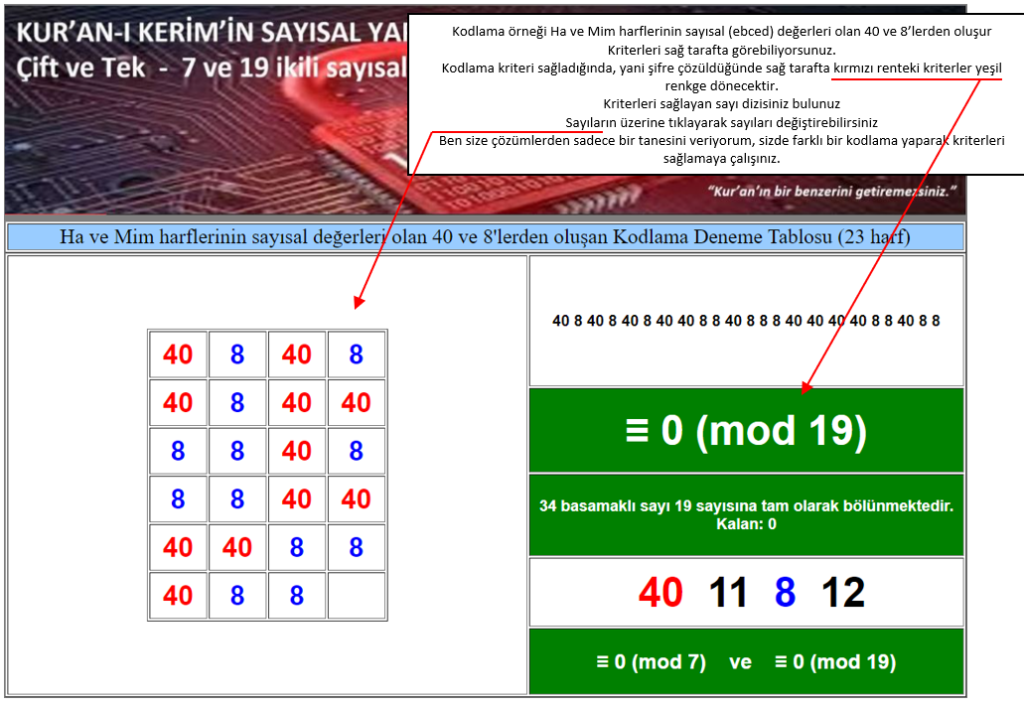
12. 13. ve 14. kriterleri oluşturan ikinci grup kodlamalar Ha ve Mim surelerindeki kodlama harflerinin sayısal (ebced) değerlerinin, harflerin sureler içindeki dizilimleri üzerinde ortaya çıkan kodlamalardır. Kodlama detaylarını aşağıda verdiğim linklerdeki Youtube videolarında izleyebilirsiniz.
Kodlamaların iyi anlaşılması için sizlere mikro örnekler hazırladım. Deneyerek kodlamanın nasıl bir şey olduğunu, seviyelerin birbirleriyle bağlantılarını, kriterlerin nasıl birbirlerini etkilediklerini, nasıl bir matematiksel zorluk barındırdığını çok daha yakından görebilirsiniz.
DENEME YAPABİLECEĞİNİZ MİKRO KODLAMALAR
Basit seviye Ha-Mim (23 Harf) Denemelerinizi buradan yapabilirsiniz.
A serisinde bir çözüm öneriyorum. Konuyu anlamanızı kolaylaştıracaktır.
Seviye – A1 için 40 11 8 12 ve Seviye – A2 için 6 2 4 4 1 6 sayılarını kullanın.
Seviye – A1 Seviye – A2 Seviye – A3
A serisine sadece bir kriter daha eklenerek B serisi oluşturulmuştur. Eklenen yeni basit bir kriterin kodlamanın zorluk derecesini ne kadar fazla arttırdığını buradan çok iyi görebileceksiniz.
A serisini tamamlayanlar, bu aşamada kodlamanın sistematiğini çözenler, mutlaka B serisini de denesinler. Matematiksel zorluğun nasıl arttığını görsünler. Böylece Kur’an orijinal kodlamasındaki durumu daha iyi değerlendirebileceklerdir.
Seviye – B1 Seviye – B2 Seviye – B3 Seviye – B4
23 harflik mikro kodlamayı çözdüyseniz, olayı anlamaya başladınız demektir. Matematiksel zorluğun nasıl logaritmik olarak arttığını görmek için aşağıdaki 55 harfli A-serisini çözmeye çalışın ve Seviye – A3’den sonra Seviye – B4’e geçerken eklenen kriterin matematiksel zorluğu nasıl arttırdığına şahit olun.
Orta seviye Ha-Mim (55 Harf) Denemelerinizi buradan yapabilirsiniz.
Seviye – A1 Seviye – A2 Seviye – A3
Seviye – B1 Seviye – B2 Seviye – B3 Seviye – B4
İleri seviye Ha-Mim (90 Harf) Denemelerinizi buradan yapabilirsiniz.
Seviye – A1 Seviye – A2 Seviye – A3
Seviye – B1 Seviye – B2 Seviye – B3 Seviye – B4
55(5×11)harfli veya 90(9×10)harfli Deneme Kodlamasını Seviye – B4 olarak çözerek,
çözümü WEB sayfasından kendi adına tescil edenlere kitabımı hediye ediyorum

ISBN-13: 9786057034335
ISBN-10: 6057034333
Seviye – B4 kodlama çözümünü kendi adına tescil ettirenler ile
Telefon görüşmesi yapılacak ve Kitapları Kargolanacaktır
Karşınıza çıkacak tescil ekranı aşağıdaki gibidir
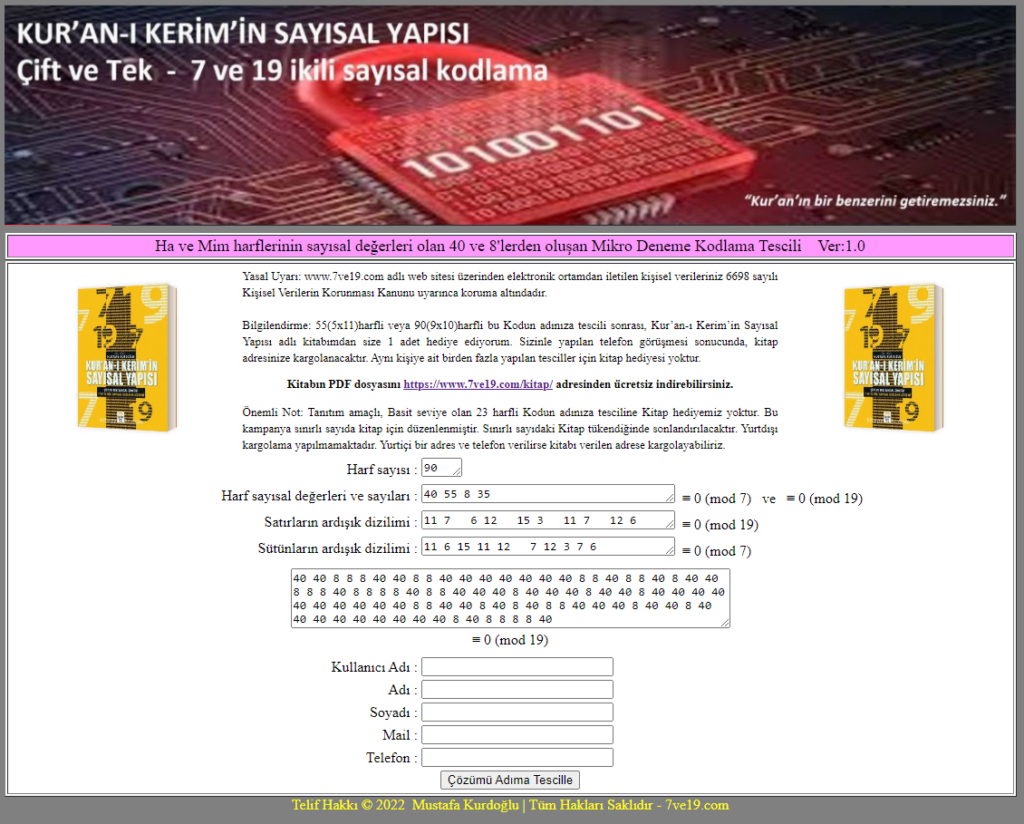
Eğer 2. grup kodlamaların nasıl oluştuğunu denemeler yaparak anladıysanız,
Kur’an orijinalinde görmek için hazırsınız demektir.
Yukarıdaki linklerden KUR’AN ORİJİNAL KODLAMALARINI deneyebilirsiniz.
Kur’an Orijinal Kodlaması Ha-Mim (2147 harf)
Bunun nasıl olabildiğini açıklayacak,
bir benzerini getiririm diyen ADAM aranıyor.
——————————————————————————————-
Ha-Mim ve Ayn-Sin-Kaf Birlerşimi
Basit seviye Ha-Mim ve Ayn-Sin-Kaf Birleşimi (29 Harf) Denemelerinizi buradan yapabilirsiniz.
Kur’an Orijinal Kodlaması
Ha-Mim ve Ayn-Sin-Kaf Birleşimi (2356 Harf).
3- Grup Kodlamalar:
Üçüncü grup kodlamalar Ha ve Mim surelerindeki kodlama harflerinin ayetlere dağılımlarından ortaya çıkan sayısal tablolarda ortaya çıkan kodlamalardır. Kodlama detaylarını aşağıda verdiğim linklerdeki Youtube videolarında izleyebilirsiniz.







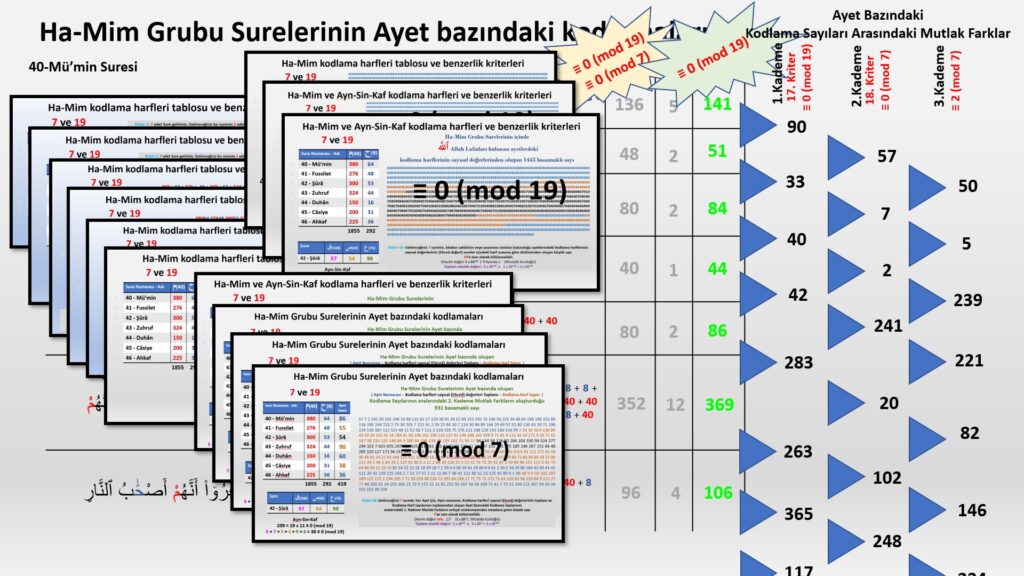
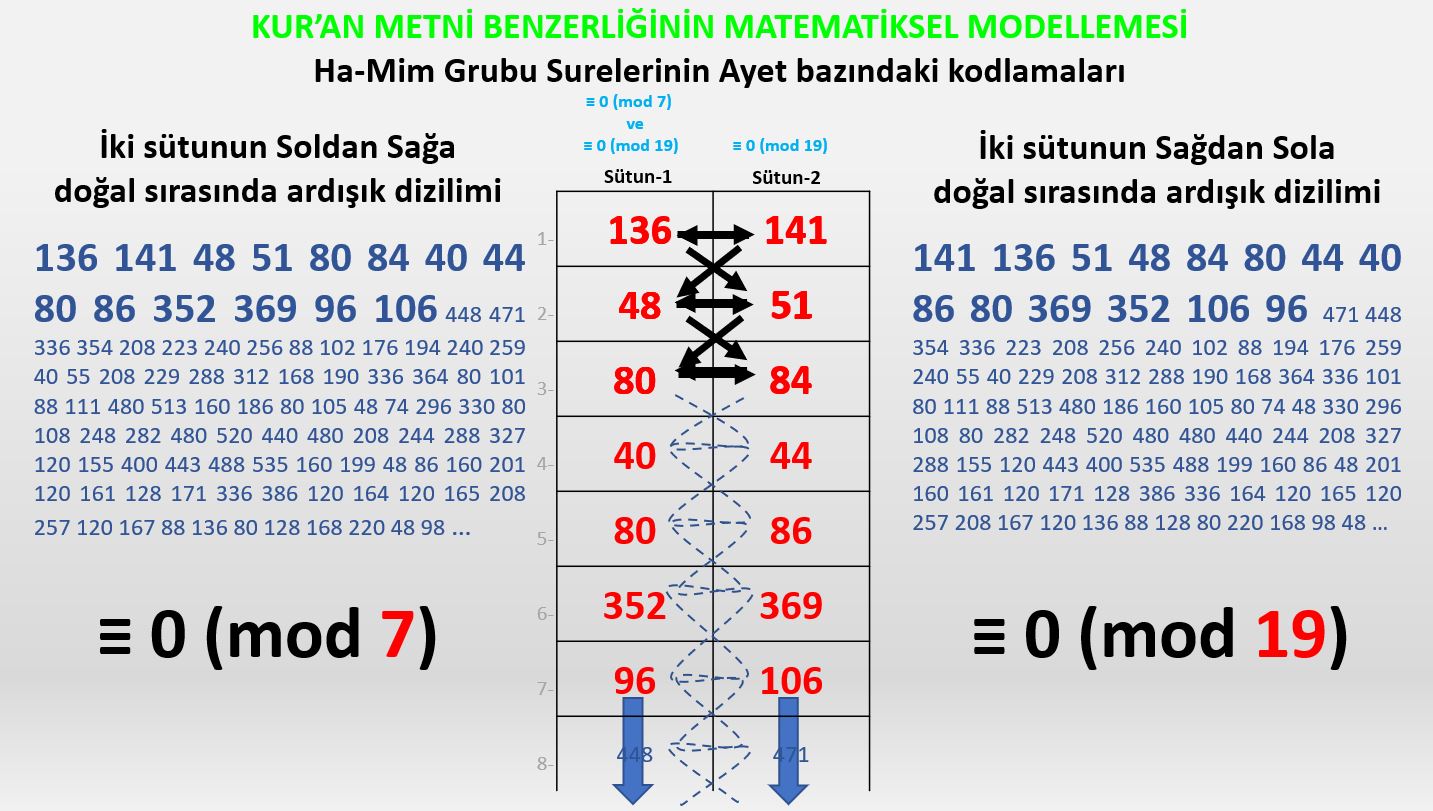
1.Grup kodlamalara Örnekler:
Kriteri sağlayan benim bulduğum sayı dizileri:
2. kriter: 330 33 176 28 275 48 635 39 251 47 281 67 296 40
3. kriter: 425 33 176 28 275 48 635 48 251 47 281 67 410 50
4.1 ve 4.2 kriterler: 240 71 230 94 260 93 219 51 307 71 299 41 300 80
4.3 ve 4.4 kriterler: 240 71 230 94 260 93 307 61 219 80 308 42 291 41
5. kriter: 240 71 377 24 113 30 307 61 234 16 341 37 250 65
6. kriter: 240 33 230 94 260 93 307 61 219 80 291 41 308 42
İlk 10 kriteri sağlayan benim bulduğum sayı dizileri:
Birinci örnek : 100 40 313 37 123 90 390 92 206 30 339 18 304 65
İkinci örnek : 475 64 150 32 426 88 309 40 110 42 123 17 221 50
Üçüncü örnek : 304 83 150 13 426 88 324 44 122 30 123 17 392 31
Dördüncü örnek: 240 71 377 24 113 30 307 61 234 16 432 44 175 23